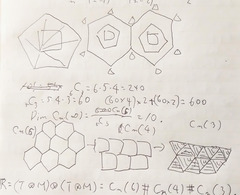hypographさんとモバ友になろう!
日記・サークル・友達・楽しみいっぱい!
-
- 2025/5/21 17:44
- 今日の数式
-
- コメント(0)
- 閲覧(4)
-

-
- 階乗をその前の階乗とその前の数での掛け算や割り算で表記する行列が、その階乗と幾つかを除き表し得る事に気付き、その6と4と3の時、階乗は、順番なく入れ替わった場合の数なので、六角形と四角形と三角形については、以下の通りです。
│× 120 24 6 ×││(×)×××(×)│=720
│6 × 4 3 2││÷(×)÷÷÷│
│× × 6 2││(×)(×)××│=120
│5 × × 2││×(×)(×)×│
│× 6 2││(×)××│=24
│× × 2││(×)(×)×│
│× ×││(×)(×)│=6
│3 2││××│
多角形の交点を持たない対角線の個数のカタラン数(ここでは、Cn.)とその因数分解の数Geodeジオードは、群や体のように5次の多項式で計算されるというので、その平面で出る六角形と四角形と三角形について貼り合わせられないかと考えておりました。もはや、次数なのか、平面の数字なのか分からなくなりましたが、解があるかと存じます。
若し、5次の多項式の解が求積的に求められるのであれば、その微分は、5次の微分式、強いては、五体問題に繋がるかと存じております。
では、またの機会にお目に掛かりましょう。
- 階乗をその前の階乗とその前の数での掛け算や割り算で表記する行列が、その階乗と幾つかを除き表し得る事に気付き、その6と4と3の時、階乗は、順番なく入れ替わった場合の数なので、六角形と四角形と三角形については、以下の通りです。