M(y^o^μ)#eSさんの日記

更新する

- 2010/12/13 15:21
- 角度の問題(ヒント&解答)
- コメント(3)
- 閲覧(20)
- ﾋﾝﾄ無しで解きたい方はこちらへ
  『ﾘﾝｸ:角度の問題(数学)/M(y^o^μ)#eS』
  　
  　
  　
  ﾋﾝﾄ
  わからない角度を埋めていくだけでは解けません。
  角Xについて方程式を立てましょう。
  　
  　
  ･方程式の立て方
  　
  ﾋﾝﾄ1　角Xを含む2つの三角形について、三角比を使いましょう(数学Ⅰ)
  図中に辺の長さの記載がなく、角度の情報がないから使う定理は…？
  　
  ﾋﾝﾄ2　なんだか図の中に二等辺三角形があるようですね。
  　
  　
  >方程式は立てたけど解けない方
  加法定理を用いたあの公式です(数学Ⅱ)
  　
  　
  ﾋﾝﾄを元に解きたい方は戻るべし(以下解答)
  　
  　
  　
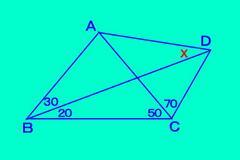
  【解答】
  求める角度をX=∠ADBとする。
  ∠ABC=∠ACB=より、AB=AC…①
  　
  △ABDについて正弦定理より
  sinX/AB=sin30ﾟ/AD
  AD/AB=sin30ﾟ/sinX…②
  　
  △ACDについて正弦定理より
  sin(X+40ﾟ)/AC=sin70ﾟ/AD
  AD/AC=sin70ﾟ/sin(X+40ﾟ)
  …③
  　
  ①②③より
  sin30ﾟ/sinX=sin70ﾟ/sin(X+40ﾟ)
  sin30ﾟsin(X+40ﾟ)=sin70ﾟsinX
  　
  ※和積の公式(積→和)より
  cos(30ﾟ+X+40ﾟ)-cos(30ﾟ-X-40ﾟ)=cos(70ﾟ+X)-cos(70ﾟ-X)
  cos(X+70ﾟ)-cos(-X-10ﾟ)=cos(70ﾟ+X)-cos(70ﾟ-X)
  cos(X+10ﾟ)=cos(70ﾟ-X)
  cos(X+10ﾟ)-cos(70ﾟ-X)=0
  　
  ※和積の公式(和→積)より
  cos(X+10ﾟ)-cos(70ﾟ-X)
  =-2sin40ﾟsin(2X-60ﾟ)
  　
  -2sin40ﾟsin(2X-60ﾟ)=0より
  2X-60ﾟ=0
  　[補足
  　0ﾟ<X<110ﾟより
  　-60ﾟ<2X-60ﾟ<160ﾟであり、
  　これを満たす
  　sin(2X-60ﾟ)=0は
  　2X-60ﾟ=0のみ]
  X=30ﾟ
  　
  　
  …ちなみに俺は全く解けませんでした←
  正弦定理使うんですか…こんなん思い付くかヽ(｀Д´)ﾉみたいな。
  …打つのがんばった俺　
  　
  　
  以下補足知識
  　
  ※和積の公式の導き方
  　cos(A+B)=cosAcosB-sinAsinB
  -)cos(A-B)=cosAcosB+sinAsinB
  ――――――――――――――
  　cos(A+B)-cos(A-B)=-2sinAsinB
  sinAsinB=-{cos(A+B)-cos(A-B)}/2〃(積→和)
  　
  ここでα=A+B、β=A-Bとすると
  A=(α+β)/2
  B=(α-β)/2
  上記の
  cos(A+B)-cos(A-B)=-2sinAsinB
  より
  cosα-cosβ=-2sin{(α+β)/2}sin{(α-β)/2}〃(和→積)